Elementary Number Theory

Thursday, April 9, 2009

Representation Of Integers

Given an integer b>1,any positive integer N can be written uniquely in tems of powers of b as

$N=a_{m}b^{m}+a_{m-1}b^{m+1}+....+a_{2}b^{2}+a_{1}b+a_{0}$

where the coefficient $0\leq a_{k}\leq b-1$ .

Example 1

N=10,b=2

First step.
10=5•2+0
5=2•2+1
2=1•2+0

Second step.
Let b=2.

$10=5\cdot b+0=(2\cdot b+1)\cdot b=2\cdot b^{2}+1\cdot b=(1\cdot b)\cdot b^{2}+1\cdot b=1\cdot b^{3}+1\cdot b=1\cdot 2^{3}+1\cdot 2$

Example 2

Let N=105,b=3.
105=35•3+0
35=11•3+2
11=3•3+2
3=1•3+0

Let b=3.
$105=35\cdot b+0=(11\cdot b+2)\cdot b=11\cdot b^{2}+2\cdot b=(3\cdot b+2)\cdot b^{2}+2\cdot b=3\cdot b^{3}+2\cdot b^{2}+2\cdot b=(1\cdot b)\cdot b^{3}+2\cdot b^{2}+2\cdot b=1\cdot b^{4}+2\cdot b^{2}+2\cdot b$

$\therefore 105=1\cdot 3^{4}+2\cdot 3^{2}+2\cdot 3$

Myspace
Graphics- At Myspacejunks.com

salam to all readers...

have you all heard about the documentary about THE ARRIVAL? If not, now you can watch it from our page! Its a documentary video that have been done by a muslim just for da'wah. Its very interesting and you can learn a lot from it. let me briefly give you the introduction about the documentary. This documentary revealed about our world today that have been ruled long time ago by the companion of DAJJAL (the arrival). Its tell us how they work,for who they work,what are their goals,why they make all this and the most important thing is are we well prepared to face all this obstacles to fight them..?? If you all want to know more about this documentary, check out their website at www.wakeupproject.com.

The Theory Of Congruences.

Definition.

Let n be a fixed positive integer. Two integer are said to be congruent modulo n,symbolized by $a\equiv b (mod n)$ (pronounced a congruent to b modulo n)if n|a-b. If it's not,hence a is said to be not congruent to b modulo n.

Example:
Let say a=7,b=10 and n=3.

Since 7-10=-3 and -3|3,hence $7\equiv 10(mod 3)$ .

Theorem 14 - For any integers a and b, $a\equiv b(mod n)$ if and only if a and b leave the same nonnegative remainder when divided by n.

Theorem 15 - Len n be fixed and a,b,c and d can be any integers. The following properties hold

a) $a\equiv a(mod n)$

b) If $a\equiv b(mod n)$ ,then $b\equiv a(mod n)$

c) If $a\equiv b(mod n)$ ,and $b\equiv c(mod n)$ ,then $a\equiv c(mod n)$ .

d) If $a\equiv b(mod n)$ ,and $c\equiv d(mod n)$ ,then $a+c\equiv b+d(mod n)$ and $ac\equiv bd(mod n)$ .

e) If $a\equiv b(mod n)$ ,then $a+c\equiv b+c(mod n)$ and $ac\equiv bc(mod n)$ .

f) If $a\equiv b(mod n)$ ,then $a^{k}\equiv b^{k}(mod n)$ for any k>0.

Proof

a) Since a-a=0,and n|0,hence $a\equiv a(mod n)$ .

b) Suppose that $a\equiv b(mod n)$ . So from the definition,n|a-b. It follows that a-b=nk for some k. Since b-a=-nk,we multiply both side by -1,we'll ontain -b+a=a-b=nk. So,n|a-b,thus $b\equiv a(mod n)$ .

c) Suppose that $a\equiv b(mod n)$ and $b\equiv c(mod n)$ . So from the definition,n|a-b and n|b-c. It follows that a-b=nk for some k and b-c=nj for some j. By substituting b=a-nk into b-c=nj,we'll obtain a-nk-c=nj. So a-c=nj+nk. From that we get a-c|n and thus $a\equiv c(mod n)$ .

d) Suppose that $a\equiv b(mod n)$ and $c\equiv d(mod n)$ . From the definition,n|a-b and n|c-d. It follows that a-b=nk for some k and c-d=nj for some j.

a-b + (c-d) = nk + nj
a-b + c-d = n (k+j)
a+c - b-d = n (k+j)
a+c - (b+d) = n (k+j)

Because a+c - (b+d)|n,hence $a+c\equiv b+d(mod n)$ .

ac-bd=ac-bc+bc-bd
=c(a-b)+b(c-d)
=c(nk)+b(nj)
=n(ck-bj)

Because n|ac-bd,therefore $ac\equiv bd(mod n)$ .

e) Since $a\equiv b(mod n)$ ,we know n|a-b.

a-b=(a+c)-(b+c)

Hence n|(a+c)-(b+c). So, $a+c\equiv b+c(mod n)$ .

Since $a\equiv b(mod n)$ ,we know n|a-b.

ac-bc = c(a-b)

Hence n|c(a-b). So, $ac\equiv bc(mod n)$ .

Myspace
Graphics- At Myspacejunks.com

FINAL EXAM!!!!!!!

To all our beloved classmates (082's CTS) and everybody who's gonna sit for the final exam,

Number Theory Brothers wish u good luck in your final exam. Pray for our success.

Tuesday, April 7, 2009

Typical Kampong Problem..blergh!

During school holiday,Pak Hamid offers Hakimi to do a part time jobs to get an extra pocket money. He’ll pay RM 14 per hour for the painting his house and RM21 per hours to take care of his farm. By the end of the school holiday,Hakimi get a well paid RM147 from Pak Hamid. How many hours possible did Hakimi spend for each of the respective job?

Myspace Graphics

Solution.

The equation derived is 21x + 14y = 147

Let x represent the hours spent for taking care of Pak Hamid’s farm.
Let y represent the hours spent for the painting job.

Using Euclidean Algorithm we evaluate gcd(21,14)
21 = 1•14 + 7
14 = 2•7 + 0

Hence,the gcd(21,14) equals to 7.

Since gcd(21,14) equals to 7 and 7|147,hence the equation 21x+14y=147 has a solution.

To obtain the integer 7 as a linear combination of 21 and 14,we work backward from the previous computation as follows:
7 = 21 - 1•14

Hence,7=1•21- 1•14

Upon multiplying this equation by 21,we obtain
147 = 21•21+(-21)•14

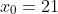
Thus, $x_{0}=21$ and $y_{0}=-21$ .
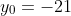
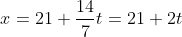
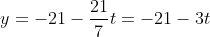
The general solution of 21x+14y=147 is given by the equation $x=21+\frac{14}{7}t=21+2t$ and $y=-21-\frac{21}{7}t=-21-3t$

Since x and y represent time,hence it cannot be negative.

21+2t>0 and -21-3t>0
Hence,
t>-10.5 and t<-7.

The overlapped real value of t is -8,-9 and -10.
Substitute the value of t obtained to the general solution of x and y,we’ll get;
When t=-8,x=5 and y=3
When t=-9,x=3 and y=6
When t=-10,x=1 and y=9.

Myspace Graphics

Monday, April 6, 2009

lets get to the basic..

fun math : exciting..!!!!

Thursday, April 2, 2009

2 = 1? Explain please,Prof. Hafiz..

Given

$x^{2}=xy$ Multiply both sides by X

$x^{2}-y^{2}=xy-y^2{}$ Subtract Y^2 from both sides

Factor both sides

Cancel out common factors

Substitute in from line (1)

Collect the Y's

Divide both sides by Y

Now obviously, 2 doesn't equal 1. So what's wrong with this proof?

Answer
'Cancelling' the common factors from line (4) to (5) means dividing by the factor (X-Y). Since X=Y, this is a division by 0, the results of which are undefined.